Элементарные преобразования матриц и их свойства. Матричная алгебра - элементарные преобразования матриц Элементарные преобразования столбцов матрицы

Введем понятие элементарной матрицы.

ОПРЕДЕЛЕНИЕ. Квадратная матрица, получающаяся из единичной матрицы в результате неособенного элементарного преобразования над строками (столбцами), называется элементарной матрицей, соответствующей этому преобразованию.

Так, например, элементарными матрицами второго порядка являются матрицы

где А - любой ненулевой скаляр.

Элементарная матрица получается из единичной матрицы Е в результате одного из следующих неособенных преобразований:

1) умножение строки (столбца) матрицы Е на отличный от нуля скаляр;

2) прибавление (или вычитание) к какой-либо строке (столбцу) матрицы Е другой строки (столбца), умноженной на скаляр.

Обозначим через матрицу, получающуюся из матрицы Е в результате умножения строки на ненулевой скаляр А:

Обозначим через матрицу, получающуюся из матрицы Е в результате прибавления (вычитания) к строке строки, умноженной на А;

Через будем обозначать матрицу, получающуюся из единичной матрицы Е в результате применения элементарного преобразования над строками; таким образом, есть матрица, соответствующая преобразованию

Рассмотрим некоторые свойства элементарных матриц.

СВОЙСТВО 2.1. Любая элементарная матрица обратима. Матрица, обратная к элементарной, является элементарной.

Доказательство. Непосредственная проверка показывает, что для любого отличного от нуля скаляра А. и произвольных выполняются равенства

На основании этих равенств заключаем, что имеет место свойство 2.1.

СВОЙСТВО 2.2. Произведение элементарных матриц является обратимой матрицей.

Это свойство непосредственно следует из свойства 2.1 и следствия 2.3.

СВОЙСТВО 2.3. Если неособенное строчечное элементарное преобразование переводит -матрицу А в матрицу В, то . Верно и обрсипное утверждение.

Доказательство. Если есть умножение строки на ненулевой скаляр А, то

Если же , то

Легко проверить, что верно также обратное утверждение.

СВОЙСТВО 2.4. Если матрица С получается из матрицы А при помощи цепочки неособенных строчечных элементарных преобразований , то . Верно и обратное утверждение.

Доказательство. По свойству 2.3, преобразование переводит матрицу А в матрицу переводит матрицу в матрицу и т. д. Наконец, переводит матрицу в матрицу Следовательно, .

Легко проверить, что верно и обратное утверждение. Условия обратимости матрицы. Для доказательства теоремы 2.8 необходимы следующие три леммы.

ЛЕММА 2.4. Квадратная матрица с нулевой строкой (столбцом) необратима.

Доказательство. Пусть А - квадратная матрица с нулевой строкой, В - любая матрица, . Пусть - нулевая строка матрицы А; тогда

т. е. i-я строка матрицы АВ является нулевой. Следовательно, матрица А необратима.

ЛЕММА 2.5. Если строки квадратной матрицы линейно зависимы, то матрица необратима.

Доказательство. Пусть А - квадратная матрица с линейно зависимыми строками. Тогда существует цепочка неособенных строчечных элементарных преобразований, переводящих А в ступенчатую матрицу; пусть такая цепочка. По свойству 2.4 элементарных матриц, имеет место равенство

где С - матрица с нулевой строкой.

Следовательно, по лемме 2.4 матрица С необратима. С другой стороны, если бы матрица А была обратимой, то произведение слева в равенстве (1) было бы обратимой матрицей, как произведение обратимых матриц (см. следствие 2.3), что невозможно. Следовательно, матрица А необратима.

Матрица, виды матриц, действия над матрицами.

Виды матриц:

1. Прямоугольные : m и n - произвольные положительные целые числа

2. Квадратные : m=n

3. Матрица строка : m=1 . Например, (1 3 5 7) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец : n=1 . Например

5. Диагональная матрица : m=n и a ij =0 , если i≠j . Например

6. Единичная матрица : m=n и

7. Нулевая матрица : a ij =0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица : все элементы ниже главной диагонали равны 0.

9. Симметрическая матрица :m=n и a ij =a ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA"=A

Например,

10. Кососимметрическая матрица : m=n и a ij =-a ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a ii =-a ii )

Действия над матрицами:

1. Сложение

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A mk *B kn =C mn причем каждый элемент с ij матрицы C mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Транспонирование матрицы А. Транспонированную матрицу обозначают A T или A"

,например

Строки и столбцы поменялись местами

Свойства операций над матрицами:

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(λA)"=λ(A)"

(A+B)"=A"+B"

(AB)"=B"A"

2. Определители второго и третьего порядка (основные понятия, св-ва, вычисления)

Свойство 1. Определитель не изменяется при транспонировании, т.е.

Доказательство.

Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

Свойство 2 . При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

Доказательство.

Свойство 3. Определитель, имеющий нулевую строку, равен 0.

Доказательство этого свойства следует из свойства 2 при k = 0.

Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.

Свойство 5 . Определитель, две строки которого пропорциональны, равен 0.

Доказательство следует из свойств 2 и 4.

Свойство 6 . При перестановке двух строк определителя он умножается на –1.

Доказательство.

Свойство 7.

Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.

Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Минор. Алгебраическое дополнение. Теорема Лапласа.

Метод приведения к треугольному виду заключается в таком преобразовании данного определителя, когда все элементы его, лежащие по одну сторону одной из его диагоналей, становятся равными нулю.

Пример 8. Вычислить определитель

приведением к треугольному виду.

Решение. Вычтем первую строку определителя из остальных его строк. Тогда получим

Этот определитель равен произведению элементов главной диагонали. Таким образом, имеем

Замечание. Всё рассмотренное выше можно обобщить для определителей n-го порядка.

Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов.

Элементарными преобразованиями матрицы называются следующие ее преобразования:

I. Перестановка двух столбцов (строк) матрицы.

II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.

III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

Матрица , полученная из исходной матрицы конечным числом элементарных преобразований, называется эквивалентной . Это обозначается .

Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач.

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля (ведущий элемент ). Строку с ведущим элементом (ведущая строка ), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

Пример 1.29. Привести к ступенчатому виду матрицы

Следующие три операции называют элементарными преобразованиями строк матрицы :

1) Умножение i-й строки матрицы на число λ ≠ 0:

которое будем записывать в виде (i) → λ(i).

2) Перестановка двух строк в матрице, например i-й и k-й строк:

которую будем записывать в виде (i) ↔ (k).

3) Добавление к i-й строке матрицы ее k-й строки с коэффициентом λ:

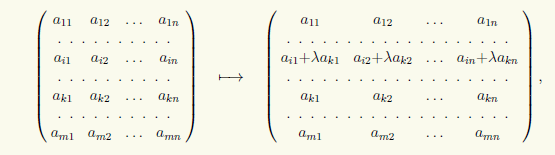
что будем записывать в виде (i) → (i) + λ(k).

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов .

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование , которое преобразованную матрицу превращает в исходную. Например, обратным преобразованием для перестановки двух строк является перестановка тех же строк.

Каждое элементарное преобразование строк (столбцов) матрицы А можно трактовать как умножение A слева (справа) на матрицу специального вида. Эта матрица получается, если то же преобразование выполнить над единичной матрицей . Рассмотрим подробнее элементарные преобразования строк.

Пусть матрица B получается в результате умножения i-й строки матрицы A типа m×n на число λ ≠ 0. Тогда B = Е i (λ)А, где матрица Е i (λ) получается из единичной матрицы E порядка m умножением ее i-й строки на число λ.

Пусть матрица B получается в результате перестановки i-й и k-й строк матрицы А типа m×n. Тогда B = F ik А, где матрица F ik получается из единичной матрицы E порядка m перестановкой ее i-й и k-й строк.

Пусть матрица B получается в результате добавления к i-й строке матрицы А типа m×n ее k-й строки с коэффициентом λ. Тогда B = G ik (λ)А, где матрица G ik получается из единичной матрицы E порядка m в результате добавления к i-й строке k-й строки с коэффициентом λ, т.е. на пересечении i-й строки и k-го столбца матрицы E нулевой элемент заменен на число λ.

Точно так же реализуются элементарные преобразования столбцов матрицы A, но при этом она умножается на матрицы специального вида не слева, а справа.

С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду. Один из важнейших таких алгоритмов составляет основу доказательства следующей теоремы.

Теорема 10.1. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду .

◄ Доказательство теоремы состоит в построении конкретного алгоритма приведения матрицы к ступенчатому виду. Этот алгоритм состоит в многократном повторении в определенном порядке трех операций, связанных с некоторым текущим элементом матрицы, который выбирается исходя из расположения в матрице. На первом шаге алгоритма в качестве текущего элемента матрицы выбираем верхний левый, т.е. [A] 11 .

1*. Если текущий элемент равен нулю, переходим к операции 2*. Если же он не равен нулю, то строку, в которой расположен текущий элемент (текущую строку), добавляем с соответствующими коэффициентами к строкам, расположенным ниже, так, чтобы все элементы матрицы, стоящие в столбце под текущим элементом, обратились в нуль. Например, если текущий элемент есть [A] ij , то в качестве коэффициента для k-й строки, k = i + 1, ... , нам следует взять число - [A] kj /[A] ij . Выбираем новый текущий элемент, смещаясь в матрице на один столбец вправо и на одну строку вниз, и переходим к следующему шагу, повторяя операцию 1*. Если такое смещение невозможно, т.е. достигнут последний столбец или строка, преобразования прекращаем.

2*. Если текущий элемент в некоторой строке матрицы равен нулю, то просматриваем элементы матрицы, расположенные в столбце под текущим элементом. Если среди них нет ненулевых, переходим к операции 3*. Пусть в k-й строке под текущим элементом находится ненулевой элемент. Меняем местами текущую и k-ю строки и возвращаемся к операции 1*.

3*. Если текущий элемент и все элементы под ним (в том же столбце) равны нулю, меняем текущий элемент, смещаясь в матрице на один столбец вправо. Если такое смещение возможно, т. е. текущий элемент находится не в самом правом столбце матрицы, то повторяем операцию 1* . Если же мы уже достигли правого края матрицы и смена текущего элемента невозможна, то матрица имеет ступенчатый вид, и мы можем прекратить преобразования.

Так как матрица имеет конечные размеры , а за один шаг алгоритма положение текущего элемента смещается вправо хотя бы на один столбец, процесс преобразований закончится, причем не более чем за n шагов (n - количество столбцов в матрице). Значит, наступит момент, когда матрица будет иметь ступенчатый вид.

Пример 10.10. Преобразуем матрицу к ступенчатому виду с помощью элементарных преобразований строк.

Используя алгоритм из доказательства теоремы 10.1 и записывая матрицы после окончания выполнения его операций, получаем

Элементарные преобразования матрицы - это такие преобразования матрицы , в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений , которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Определение

Элементарными преобразованиями строк называют:

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу , и прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов .

Элементарные преобразования обратимы .

Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот).

Свойства

Инвариантность ранга при элементарных преобразованиях

Эквивалентность СЛАУ при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений :

перестановку уравнений;
умножение уравнения на ненулевую константу;
сложение одного уравнения с другим, умноженным на некоторую константу.

Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение: Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Нахождение обратных матриц

Теорема (о нахождении обратной матрицы).
Пусть определитель матрицы не равен нулю, пусть матрица определяется выражением . Тогда при элементарном преобразовании строк матрицы к единичной матрице в составе одновременно происходит преобразование к .

Приведение матриц к ступенчатому виду

Введём понятие ступенчатых матриц: Матрица имеет ступенчатый вид , если: Тогда справедливо следующее утверждение:

Связанные определения

Элементарная матрица. Матрица А является элементарной, если умножение на нее произвольной матрицы В приводит к элементарным преобразованиям строк в матрице В.

Литература

Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов . - 6-е изд., стер. - М .: ФИЗМАТЛИТ, 2004. - 280 с.

Wikimedia Foundation . 2010 .

Смотреть что такое "Элементарные преобразования матрицы" в других словарях:

Введение. Э. ч. в точном значении этого термина первичные, далее неразложимые ч цы, из к рых, по предположению, состоит вся материя. В совр. физике термин «Э. ч.» обычно употребляется не в своём точном значении, а менее строго для наименования… … Физическая энциклопедия

Введение. Э. ч. в точном значении этого термина первичные, далее неразложимые частицы, из которых, по предположению, состоит вся материя. В понятии «Э. ч.» в современной физике находит выражение идея о первообразных сущностях,… … Большая советская энциклопедия

У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия

Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия

Определение

Элементарными преобразованиями строк называют:

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу k {\displaystyle k} , и прибавление к любой строке матрицы другой строки, умноженной на константу k {\displaystyle k} , k ≠ 0 {\displaystyle k\neq 0} .

Аналогично определяются элементарные преобразования столбцов .

Элементарные преобразования обратимы .

Обозначение указывает на то, что матрица A {\displaystyle A} может быть получена из B {\displaystyle B} путём элементарных преобразований (или наоборот).

Свойства

Инвариантность ранга при элементарных преобразованиях

Теорема (об инвариантности ранга при элементарных преобразованиях).
Если A ∼ B {\displaystyle A\sim B} , то r a n g A = r a n g B {\displaystyle \mathrm {rang} A=\mathrm {rang} B} .

Эквивалентность СЛАУ при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений :

перестановку уравнений;
умножение уравнения на ненулевую константу;
сложение одного уравнения с другим, умноженным на некоторую константу.

То есть элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение: Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Нахождение обратных матриц

Теорема (о нахождении обратной матрицы).
Пусть определитель матрицы A n × n {\displaystyle A_{n\times n}} не равен нулю, пусть матрица B {\displaystyle B} определяется выражением B = [ A | E ] n × 2 n {\displaystyle B=_{n\times 2n}} . Тогда при элементарном преобразовании строк матрицы A {\displaystyle A} к единичной матрице E {\displaystyle E} в составе B {\displaystyle B} одновременно происходит преобразование E {\displaystyle E} к A − 1 {\displaystyle A^{-1}} .

Категории

Популярное